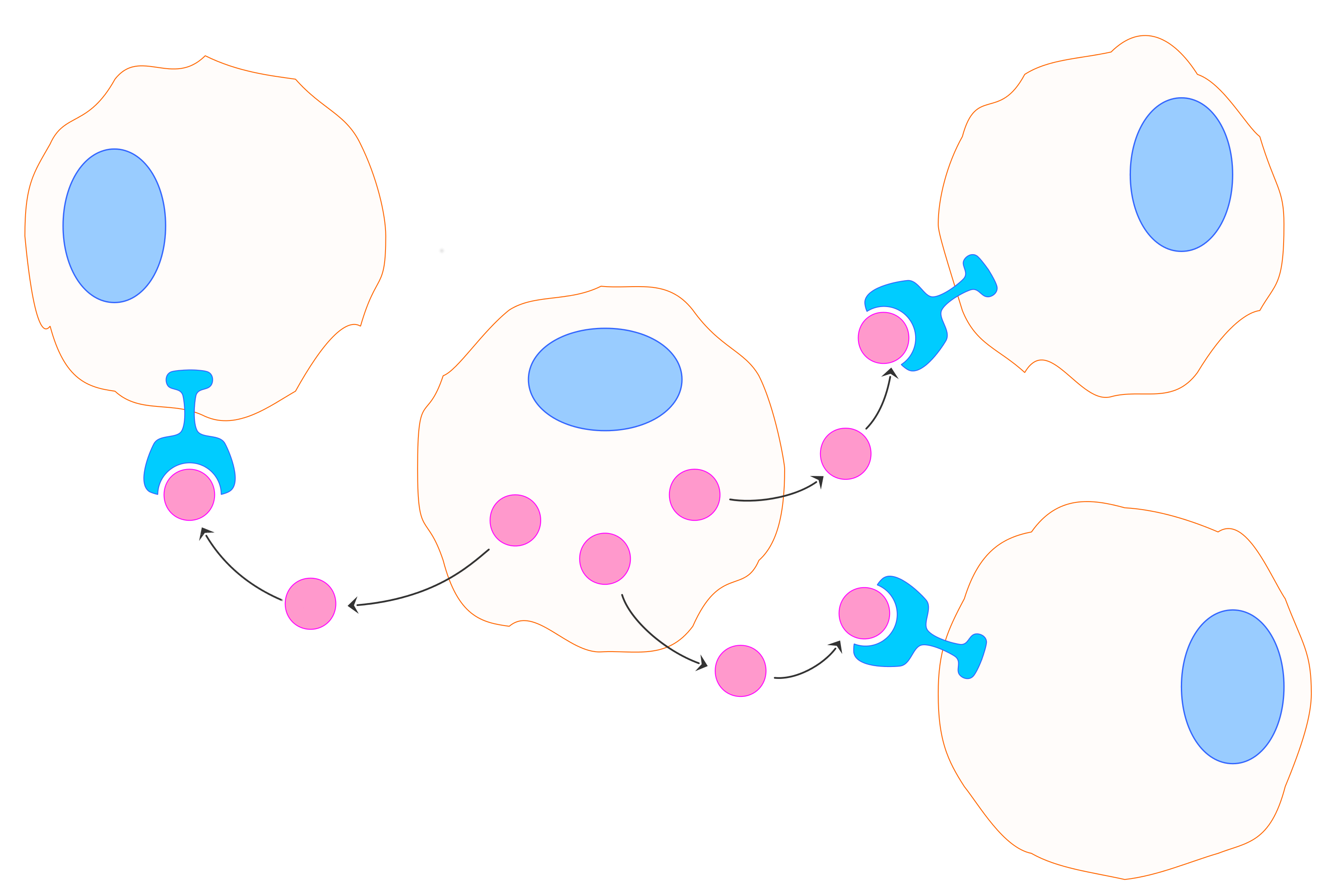
Mathematical modeling of the intracellular protein dynamics

Mathematical modelling of intracellular proteins dynamics is one of the most commonly undertaken challenges in mathematical biology. Of course, this follows from our belief that increased knowledge about these processes will allow us to better understand the functioning of a cell, especially if it is distorted, as it is in the case of many diseases like cancer. In the literature one can nd many models describing the dynamics of different proteins, however, most of these models, either ignores the spatial aspect, or treat it in a very simplied way, taking into account only the diusion as a transport mechanism of molecules. Only recently new models that take into account In this paper we propose a mathematical model of protein and mRNA transport inside a cell.

We propose the spatio-temporal model that takes into account the active transport along microtubules in the cytoplasm as well as diffusion and is able to reproduce the oscillatory changes in protein concentration observed in many experimental data. In the model the protein and the mRNA interact with each other that allows us to classify the model as a simple gene regulatory network.

Schematic representation of intracellular transport.

The proposed model is generic and may be adapted to specific signaling pathways. On the basis of numerical simulations, we formulate a new hypothesis that the oscillatory dynamics is allowed by the mRNA active transport along microtubules from the nucleus to distant locations.

Heat Shock Proteins

Heat shock proteins (HSP) are a class of very important proteins involved in many essential processes of a cell.

They are inducible by a variety of stress conditions such as heat shock, oxidative stress, fever or inflammation, the presence of alcohol, inhibitors of energy metabolism and heavy metals. It has been shown that most HSP have strong cytoprotective effects. The phenomenon of rapid and selective mRNA (coding HSP) synthesis after heat shock was first discovered in 1962 by Ritossa.

We proposed a model of HSP synthesis to explain the well-known experimental fact that in cells subjected to heat shock, one may observe a significant rise in HSP synthesis, whereas in cells subjected to slow heating (but up to the same final temperature as heat shock) such an increase in HSP synthesis is almost not visible. From computational simulation results of our model we conclude that the significant rise in HSP synthesis during heat shock is a result of accumulation of substrate (misfolded proteins), which does not occur when cells are heated slowly. Moreover, our model explains the phenomena of thermotolerance. 

Scheme of heat shock response model.

We investigated the connection between HSPs and the invasiveness of cancer cells. Inspired by experimental work which points to Hsp90 as a crucial factor influencing cancer invasion and their (at least) partial disagreement with our own experiments, we decided to use mathematical modelling as an additional tool to clarify the actual involvement of Hsp90 in this process. The results of mathematical modelling and computational simulations, supported by preliminary in vitro experiments on cancer cells, led us to formulate a new hypothesis - that the role of Hsp90 in cancer cell invasion is connected with the mediation of cell motility rather than the regulation of MDE activation and secretion. This hypothesis later gained additional experimental support. In the future, detailed studies on the impact of Hsp90 on cell motility should be performed both experimentally and theoretically using methods of mathematical modelling, analysis and simulations.

In modelling of some physical problems the idealisation concerning in entities (e.g. particles) that are concentrated in a point (mass-points), that leads to local interactions, is usually accepted. Just to give an example, this is the case in kinetic theory and the Boltzmann description of a rarefied gas. However, already in the case of more complicated that a simple rarefied gas systems a non-local type kinetic equations are used (cf. Lachowicz and Szymańska 2015 and references therein). For the biological systems it is obviously more essential to take into account the non-local interactions. 

For instance, in order to describe the phenomena of intercellular communication the nonlocal terms seem to be natural. Examples of such intercellular communication are paracrine signalling, when the cells produce chemical substances – signals – that are secreted to the extracellular space and induce changes in nearby other cells and autocrine signalling when cells produce chemical messengers that bind to the receptors on the same cells. In case of both types of signalling produced chemicals diffuse over some distance. The examples of paracrine signalling agents are various growth factors, whereas examples of autocrine signalling are various cytokines (cf. Lachowicz and Szymańska 2015).

Both types of intercellular signalling seem very important in various biological processes, in both physiological and pathological circumstances. Just mention, the production of growth factors in the healing and regeneration processes and in processes of angiogenesis and tumour growth.

Paracrine signalling.